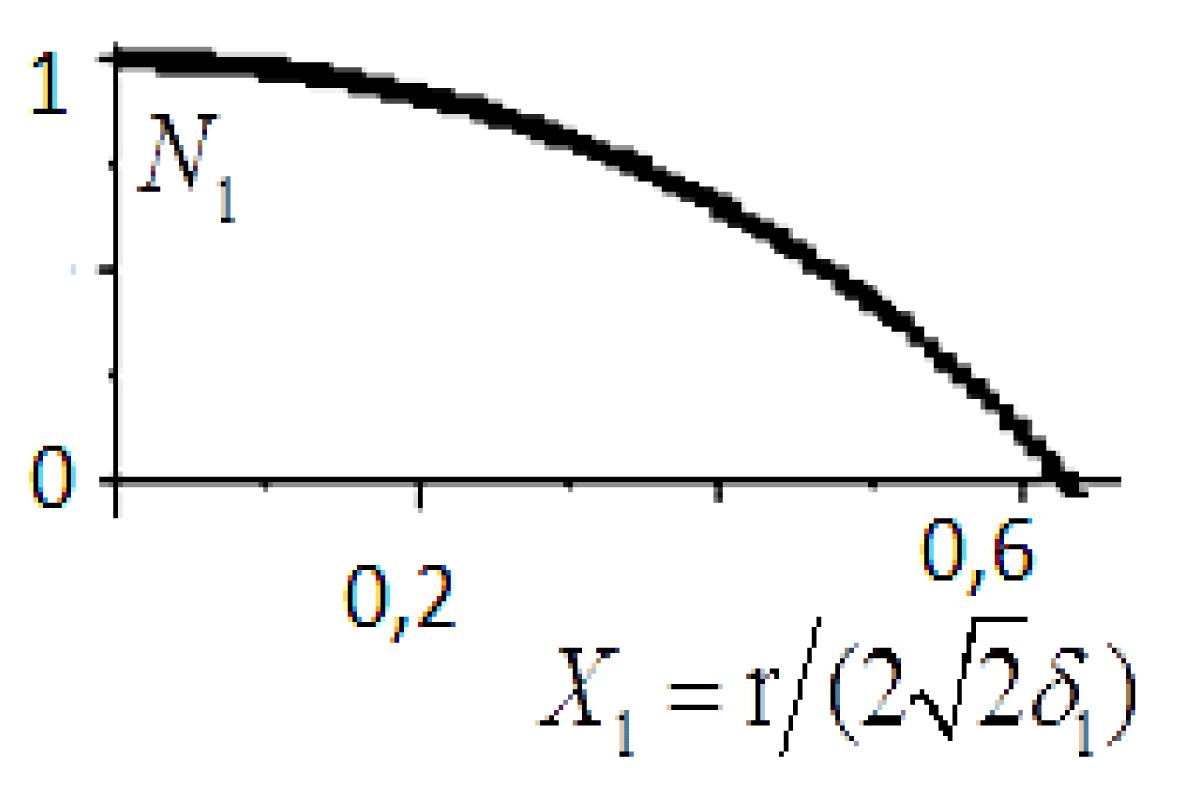More Information
Submitted: August 06, 2022 | Approved: February 13, 2023 | Published: February 14, 2023
How to cite this article: Baranov SA. Surface energy of micro- and nanowire. Ann Adv Chem. 2023; 7: 025-030.
DOI: 10.29328/journal.aac.1001039
Copyright License: © 2023 Baranov SA. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Gibbs–Tolman–Koenig–Buff theory; Tolman length; Van der Waals theory
Surface energy of micro- and nanowire
Serghei A Baranov1,2*
1Institute of Applied Physics, State University, Street Academiei 5, Chisinau, MD-2028, Republic of Moldova
2Shevchenko Pridnestrov’e State University, Street 25 Oktyabrya 128, Tiraspol, Republic of Moldova
*Address for Correspondence: Serghei A Baranov, Institute of Applied Physics, State University, str. Academiei 5, Chisinau, MD-2028, Shevchenko Pridnestrov’e State University, str. 25 Oktyabrya 128, Tiraspol, Republic of Moldova, Email: [email protected]; [email protected]
The dependence on the surface energy is important for the description of the nucleation process of micro- or nanowires. Analytical solution to Gibbs–Tolman–Koenig–Buff equation for micro- or nanowire surface is given. Analytical solutions to equations for the case of the cylindrical surface for the linear and nonlinear Van der Waals theory are analyzed.
In recent decades, micro- and nanotechnology (nano nucleation) have made substantial contributions to the significant progress in different fields, such as industries and the pharmaceutical and biomedical domains. Their advancement has led to the development of improved and new materials, tools, and devices, with various applications. Studies have generally become more interdisciplinary and complex.
Surface energy is a fundamental physical parameter and plays an important role in a variety of scientific and industrial fields. The aim of this review is to present the current state of influence of the size-dependent surface tension in micro- and nanowire.
Surface tension is a fundamental thermodynamic parameter that significantly influences the creation of micro- and nanowires.
The chemical and physical properties of interphase boundaries in nanowires, as well as for nanoparticles, have been studied in a huge number of publications (see fundamental monographs [1–5] and literature [6–9]). We can single out the following theoretical approaches: Gibbs–Tolman–Koenig–Buff equation method ends the linear and nonlinear Van der Waals theory.
The study aims at derivation and detailed analysis of expressions for the surface tension for the micro- and nanowire in thermodynamic equilibrium on the Gibbs–Tolman–Koenig–Buff equation method and on the Van der Waals theory and others theory [9].
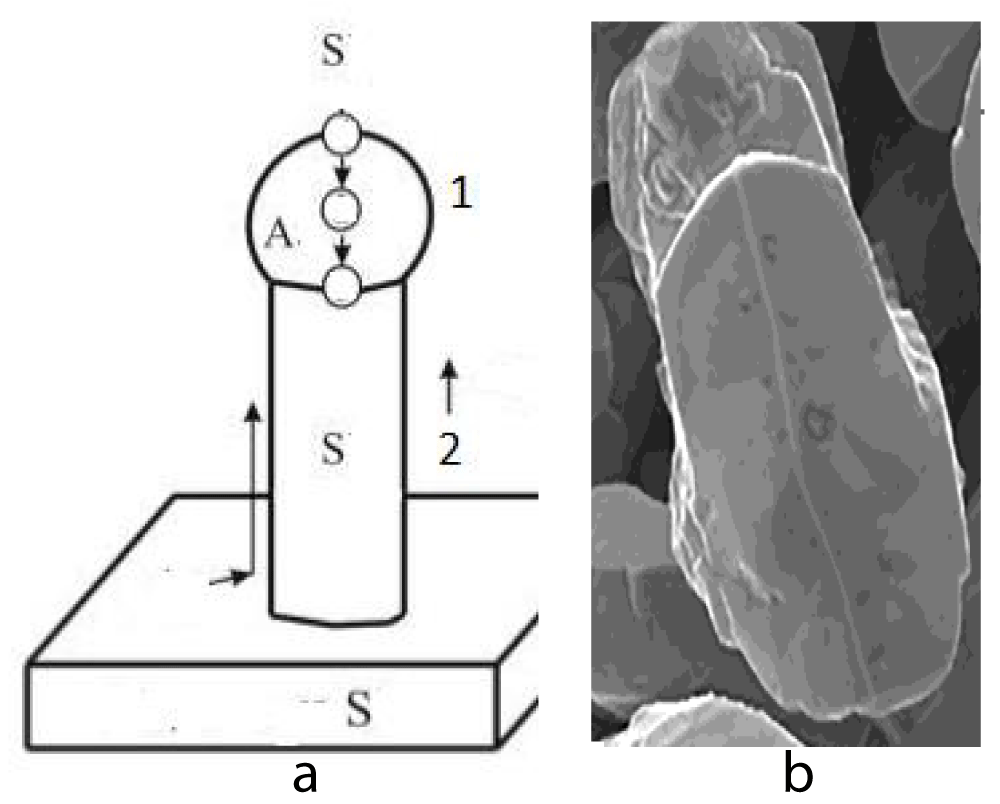
The given theory can find application in micro- and nanowire production technology (Figures 1,2)
Figure 1: a: Process of nanowires growth by the “vapor-liquid-crystal” mechanism. 1. Drops zone 2. Cylindrical zone. b: Morphology of the particles produced during electrodeposition of Co–W [6].
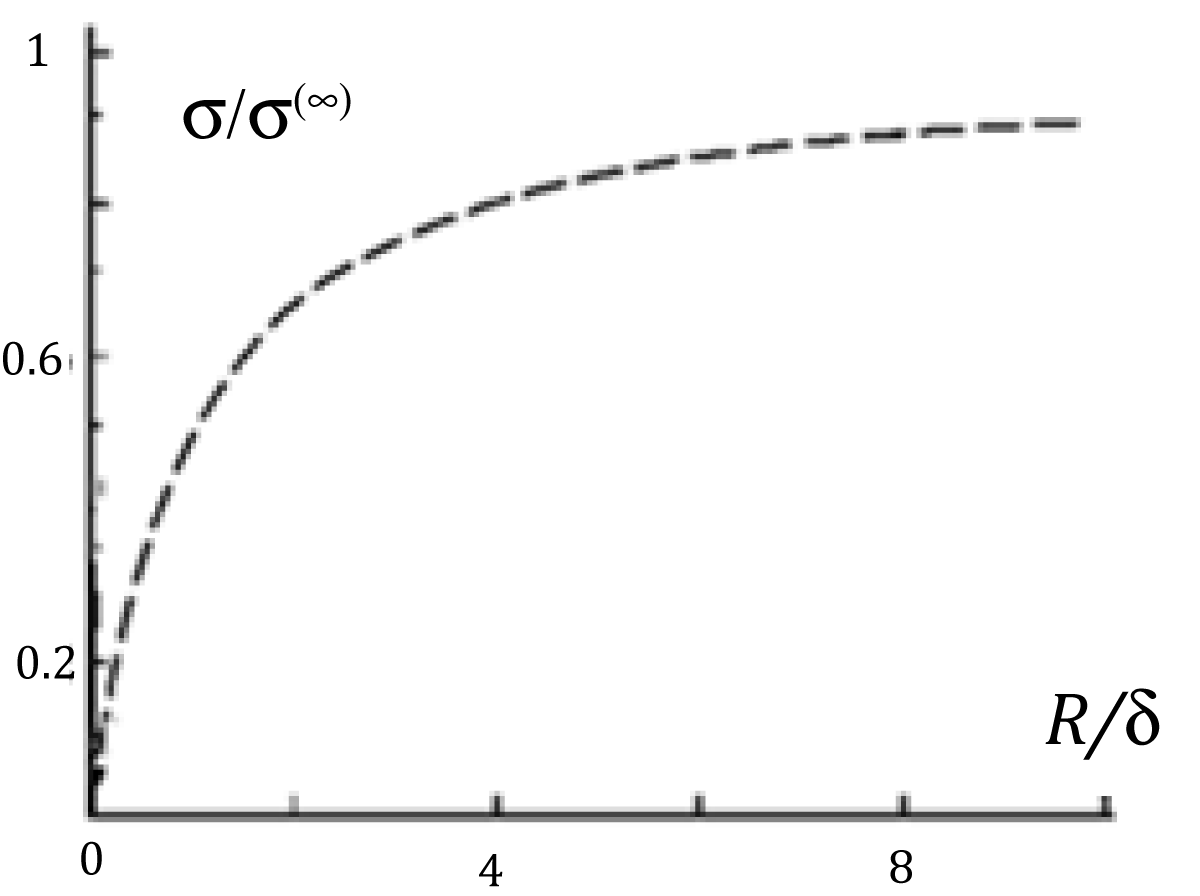
Figure 2: Functions graphs of solution (2).
We presented a growth mechanism for whiskers “vapor-liquid-crystal” (see [10]) and electrodeposition of Co–W [6].
As you can see from the figures, we must study cylindrical and conical surfaces.
Modeling of surface energy for microwires in Gibbs–Tolman– Konig–Buff`s theory
We will use the Gibbs – Tolman – Koenig – Buff differential equation [2–6] (for a cylinder) to describe the surface tensions, σi, of nanowires [1]:
(1)
Where Ri is the radii of micro- and nanowires (the radius of its metallic kernel, Rm, or the total radius of glass, Rg).
Non-negative parameters (Tolman length), δi, characterizing the thickness of the interfacial layer (for example, between glass and glass-metal).
In surface thermodynamics, the Tolman length is used as a parameter that is equal to the distance between the surface of tension and the equimolar surface. The numerical values of the parameter of the analog
“Tolman length” for micro and nanowire is in the range from 0.1 to 1 µm.
The integral in (1) (if δi =const.) can be exactly taken. The final result has the form [7,8]:
(2)
The well-known Tolman formula (for cylinder) is in a special case R >> δ for this formula (2)
(3a)
In case R << δ:
(3b)
We represent the Rusanov linear formula [5,11] for the cylindrical surface.
Modeling of surface energy for micro- and nanowires in linear Van der Waals theory
The basic equation of the linear Van der Waals theory of an inhomogeneous medium [6-8] can be written in the form:
(4)
Where n (x) is the function when proportional to the volume density N(x) (x = r/δ, no=const.), r is the radial variable measured from the center of a nanoparticle δ, and is the Tolman length [1-3].
The general solution to Eq. (4) has the form
(5)
Where are modification Bessel and Hankel functions?
(6)
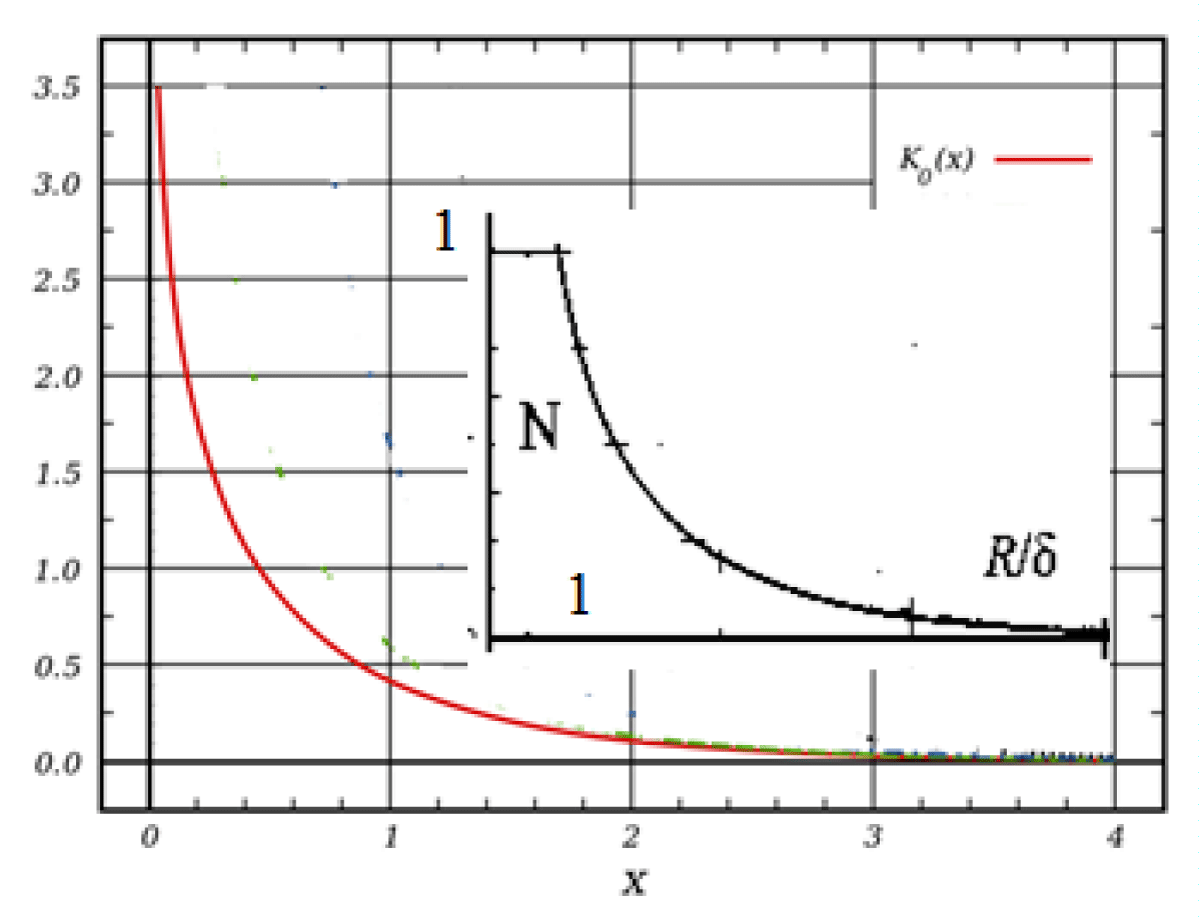
We will accept the volume density function, N(r/δ). We get:
(7)
Substituting solution (5) into expression (7) and integrating, we obtain:
(8)
We will accept the volume density function, N(r/δ)(Figure 3).
Figure 3: Functions graphs of K0(x), and volume density function, N(r/δ).
(8a)
Solution (8) can be used for calculating adsorption, which is defined as the excess number of atoms or molecules in the surface layer of the nanoparticle per unit area:
(9)
(x = r/δ, x0 = R/δ)
Taking into account adsorption (9), we obtain the differential equation
(10)
If х >> 1
(11)
We obtain
(12)
(See formula (2) and (3a));
And if х << 1
(13)
Where = 1,781 is Euler constant, we obtain
(14)
This equation is integrated numerically.
Modeling of surface energy for micro- and nanowires in nonlinear theory
The nonlinear equation can be written in the form
(15)
The simple volume density function, N, may be determined (Figure 4):
Figure 4: The function graph of solution (16) is presented.
(16)
The results obtained have a physical meaning only as long as the function N1 is positive.
The resulting density profile (see Figure 5 and (16), (17)) is very different from the results of the linear theory (see Figure 4 and (8)) and therefore the GTKB theory (see (2), (3a), (3b)).
Micro and nanowire will only be produced for a limited metallic kernel, Rm.
The long nanocylinder
We consider a case of the application theory [9] when nanoparticles have a long cylinder form. We used the cylindrical coordinate system for which the characteristic spin function [9] is presented by the angle function q(r) about the cylinder axis z.
The free energy in this model has the following form [9]:
17
Where θ(r) is the angle between the cylinder axis and the magnetization vector; r is the radial coordinate.
The model kinetic energy in (17) is a classical analog of the exchange energy in the Heisenberg model for the two-dimensional space at the continuum approximation [8] that in our case corresponds to the infinite cylinder model [9]. Then the kinetic energy in (17) coincides in form with the kinetic energy of the particle (in cylindrical coordinates). This fact is not casual as the model under consideration permits exact analytical solutions in the form of quasiparticles (nonlinear waves) which are called instantons (or skyrmions [9]). Please note that in our case these quasiparticles are not dynamic particles but topological compositions. Therefore, in our case, the virtual kinetic energy of the topological instanton is meant by the kinetic energy.
We introduce a relative coordinate:
(18)
where Rc is the drop equilibrium radius.
Then there is a condition of 0 ≤ρ≤ 1. The proposed continuum model of energy (17) actually appears as a Heisenberg model in which the interacting spins have the meaning of the energy states of the particles associated with the constant exchange interaction A (with the dimension for the exchange energy [J/m]).
Using (17) it is simple to derive the Euler - Lagrange equation:
(19)
For simplicity it is sufficient to use only a particular solution of this equation describing the nucleation process under simple boundary conditions:
(20)
The solution to problems (19), (20) has a simple form:
(21)
That is convenient for further analysis.
Let us introduce the model surface energy in order to obtain the Euler - Lagrange equations for the scale-invariant theory as well:
(22)
Where a2 is the ratio of the anisotropy energy to the exchange interaction constant A. The parameter a2 is determined in [9]:
(23)
With the determined anisotropy function (model as the Rapini modified potential [9]):
(24)
Where B is the positive energy quantity whose dimension coincides with A.
In agreement with the previous solution we assume that in (22) at B = 0, there is no anisotropy, and at B > 0 it occurs. The solution to equation (22) is as follows:
(25)
Please note that solutions (21) and (25) analytically join, therefore the indices are later omitted.
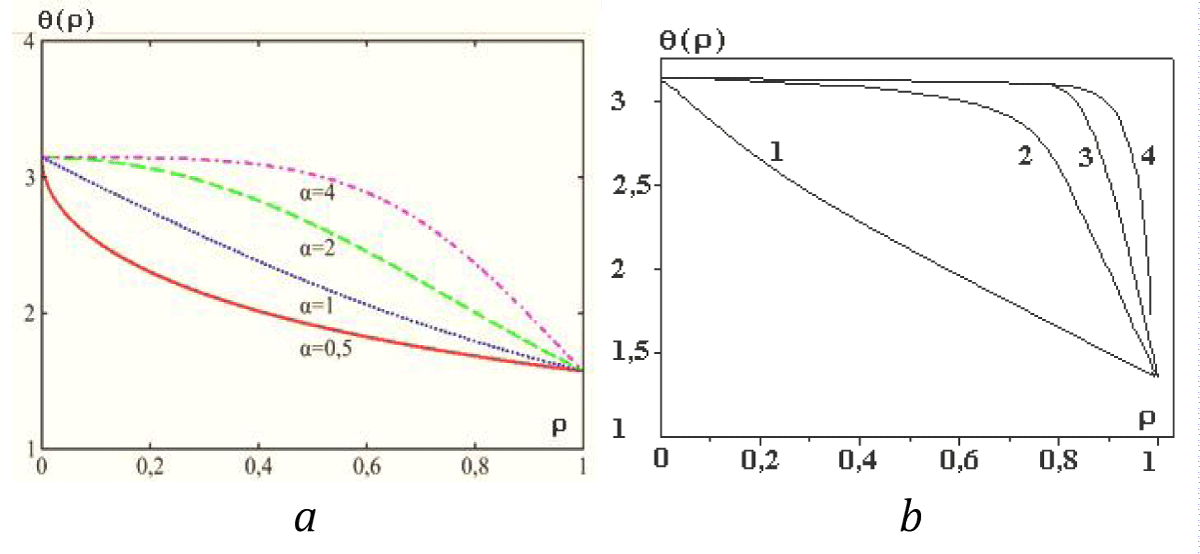
Let us consider one general solution (25). The diagram of this solution is presented in Figures 5a,b.
Figure 5: a. Diagrams of solution (25) at different values of parameter a (see [9]). b. Diagrams of solution (25) at different values of parameter a: 1 – a=1; 2 – a=10; 3 – a=50; 4 – a=100. (see [9]).
It is easy to show that the function θ(r) at a = 1 and 0 ≤ρ≤ 1has no point of inflection. This point appears only at a > 1. This means that the surface layer in our model can exist only at a > 1. In this case, some volume whose energy is the surface energy of the cylindrical particle can be chosen as a surface layer. For definiteness, we suppose, for example, that the surface layer begins to manifest itself clearly from a value of a > 4. Thus, we suppose that if a = 1 there is no anisotropy in the system, and the Tolman length actually coincides with the drop sizes. If a >> 1, then in the proposed model the specific anisotropy is more than the exchange interaction, and in the drop, there appears a parameter (the Tolman length) that characterizes the dimension of the interfacial region.
Case a < 1 corresponds to the negative surface energy (in Figure 5a. This case is presented for a = 0.5), and it is not considered in detail in this paper as it is associated with the condensed phase instability.
One can estimate the change in the free energy from the particle center to its surface. This allows the physical interpretation of the introduced parameters of the model and the comparison of them with traditional energy characteristics which are used to describe the nucleation process.
Let us initially consider the layer--by--layer change in this free energy of a cylindrical drop. Let us return to the formula for the energy which we used to derive the equation of motion. It is as follows: E(r) = T + U. Taking into account solution (9) we find that the kinetic energy is equal to the potential energy: T = U. This important result for the closed dynamic system is associated with the virial theorem for the finite motion, and in our case, it is the test if this approach to the problem solution is correct. For the total full energy we have:
(26)
It follows from (26) that at a = 1 and r < 1, the equality E(r) = A is satisfied. In the case when B > 0 the cylinder surface energy tends to Aa2 ~ B, and this limit is sharper the higher the quantity B. Thus, just this parameter B can be associated with the parameter of the specific thermodynamic surface energy which occurs in the thermodynamic theories (of Gibbs, Tolman, etc.) on the understanding that the dimension of these energies is different.
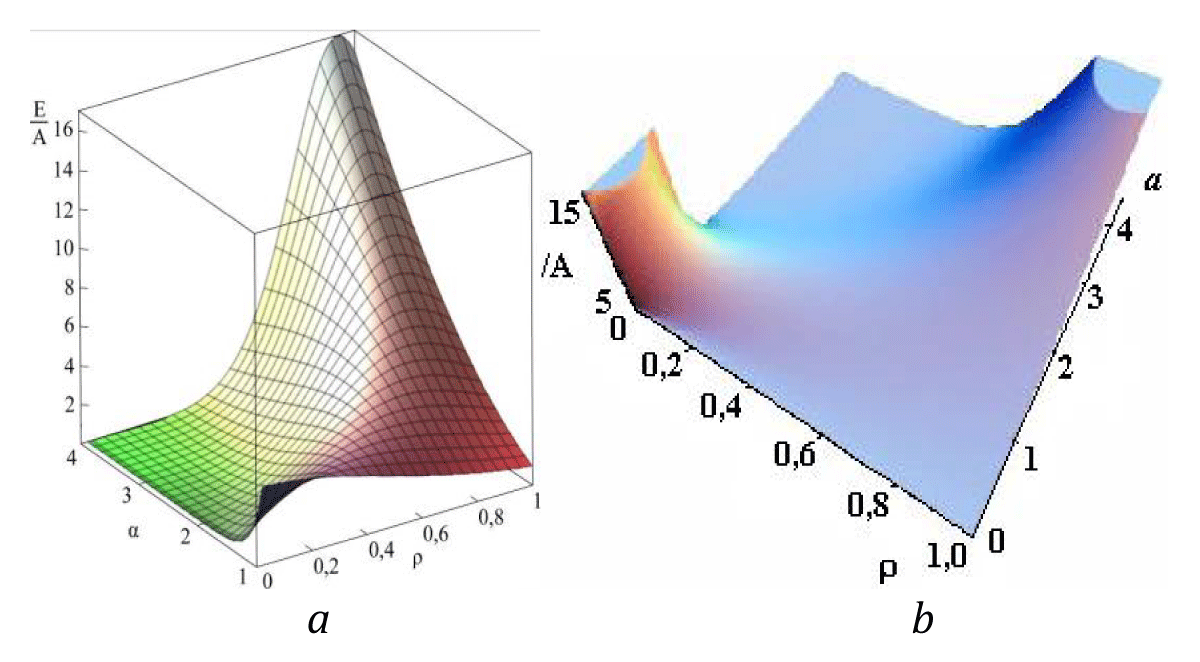
A sharp rise in free energy (see Figures 6a, b) depending on the parameter a is identified with the phase transition which takes place in the system in the case of infinitely small anisotropy [9]. In order to determine the total energy of the particle assigned to the cylinder length unit an integral of E(r) over the cylinder volume must be taken. Let us begin with a qualitative analysis of the model. Please note that for a particular case of a = 1 and В = 0, this integral must be equal to A (with an accuracy to the multiplier). Then there is no other energy in the system; here A is the only internal model energy of the system. In another limiting case, some high value of a is sufficient for the total energy to tend to the anisotropy energy B. In the general case, the total full specific energy (for the cylinder length unit) will be as follows:
Figure 6: a) Dependence of energy on parameters а and ρ (see [9]). b) Dependence of energy on parameters а and ρ (see [9]).
(27)
In the Cahn--Hillard theory [9,11,12] the activation barrier energy is in proportion to the geometric mean of two energy parameters:
(27a)
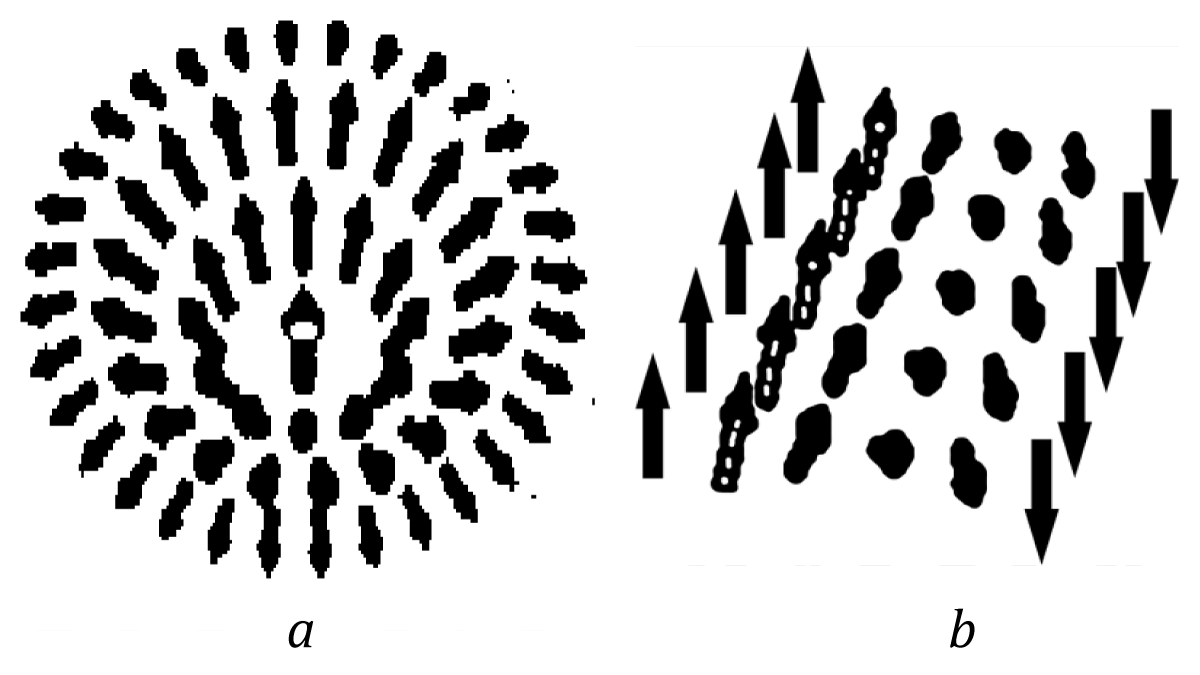
Unlike the proposed theory the Cahn--Hillard theory is not scale--invariant and the quantity B has a dimension of J/m3. In our case the integral formula derived from (11) for the activation energy has the same form, i. e., one may talk of the coincidence of these theories when calculating the mean activation energy (in the volume unit). Thus, we can deduce that the proposed theory coincides qualitatively with the Cahn - Hillard theory. In frame Cahn - Hillard theory we obtain the same analytic structures too [11,12] (Figure 7):
Figure 7: Schematics representations of the solution (25): (A), and (28): B) in the form of a domain wall of energy vectors.
(28)
The special case of a long nanocylinder
The previously introduced parameter a2 (see (23)) can formally be less than a = 1 (in Figure 5a, this case is presented for a = 0.5). This case can correspond to negative anisotropy energy, which can, for example, prevent the creation of a nanoparticle. Technologically, it is possible to initiate the creation of a nanoparticle, but limit the growth of a nanoparticle.
Therefore, it is of interest to consider the case when:
B = - A (29)
Such a physical situation can take place in the case when a nanoparticle nucleus with size ρ0 < 1 (for definiteness ρ0 = 0,1) has already been created, but its development to an equilibrium state with ρ = 1 is hindered by the created (artificially) anisotropy:
(30)
We believe that this anisotropy manifests itself only starting from some sizes corresponding to the value
ρ0 = 0,1 (31)
Then, for this case, the equation is linearized and greatly simplified:
(32)
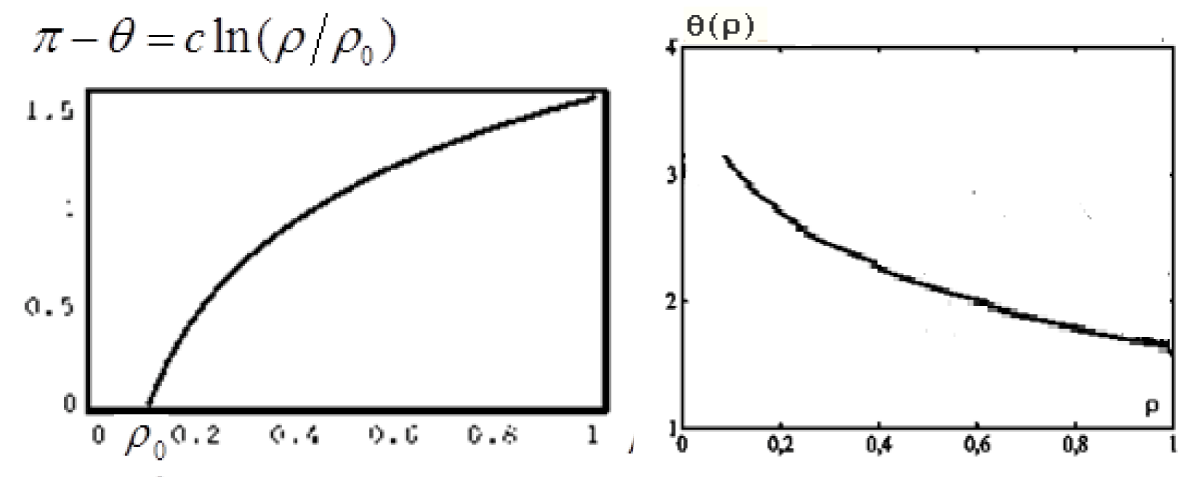
A particular solution for equation (32) can have the form (in our case, we use condition (32) to compare it with the solution in the form of the formula (25)):
(33)
Where
, (for ρ > ρ0)
The function graph is shown in Figure 8.
Figure 8: Functions graphs of the solution (33).
The surface energy is a fundamental thermodynamic parameter, which is found in the work spent on the reversible isothermal formation of the interface. Surface energy plays an important role in a variety of scientific and industrial fields. The symmetry of atomic or molecular interaction forces near the interface results in the tangential and normal components of these forces. Under the action of the force directed normally to the interface, particles are drawn into the volume of a denser phase. As a result, the tangential component acting on the particles remaining on the surface (this component tends to decrease the interfacial area and thereby is responsible for the surface tension) grows. The surface tension is, in essence, a measure of the excess free energy in the surface layer compared with the free energy in the volumes of coexisting phases
a) With the decrease of the condensed phase in size the proportion of surface atoms increases thus increasing the influence of the interphase boundaries. At the same time, the size dependence of surface tension is determined by the Tolman length i.e. the actual thickness of the interfacial (transition) layer.
b) If equations (2) (the Gibbs–Tolman–Koenig–Buff solution) can be compared with its linear analog (10) (see (12)), then the solution (16) is not reduced to linear analogs. The solution has a highly non-linear character. This nonlinearity cannot be described by perturbation theory, starting from a linear result. If the formation of nanoparticles is determined by nonlinear processes, then there is a suspicion of an incorrect description of it within the framework of the classical theory of nucleation.
c) At the end of the work there have been obtained the results associated with a special form of the van der Waals gradient theory which can be resumed in the following way. If in the formation of a nanoparticle, there is only one energy form that plays the role of the exchange interaction A then the additive separation of the system energy into the surface energy and the nanoparticle volume energy in the context of the proposed model is incorrect. However, in this case, one can introduce the average energy of the whole nanoparticle and, from simple geometric considerations, derive the Rusanov linear formula for the surface energy. Commonly, the Rusanov formula is assumed universally applicable. This fact is not confirmed when our model of the anisotropy energy is complicated.
d) The concept of the anisotropy energy, introduced into the theory in the form of the proposed model as the Rapini modified potential, leads to the appearance of the surface energy. Please note that in the conventional Rapini potential, there is no multiplier of the form 1/r2. The anisotropy energy can have the meaning of the double electric layer energy (in electrochemistry), besides, at the formation of very small equilibrium particles with the differentiated surface energy it should be increased the electric capacity of the micro- and nanocylinder where this nanoparticle is formed. So, one can suppose that the nano--nucleation process can be efficiently controlled.
e) The main findings that unite all the parts of the work are the dependences of the surface energy on the thermodynamic parameters of the system which make it possible to expand in some ways the vision of the capillary phenomena in the micro- and nanocylinder.
Despite the long history of the theory of interfacial phenomena, some of its important problems remain in dispute. In particular, this concerns the dependence of surface tension σ on interface curvature. This dependence is commonly referred to as the size dependence of surface tension. At present, there is no consensus on the character of this dependence even for the trivial case of a small spherical droplet. For example, in fundamental works [1-4], it is stated that the surface tension must decrease upon decreasing droplet radius.
This conclusion is confirmed in this work.
- Ono S, Kondo S. Molecular Theory of Surface Tension in Liquids, in Structure of Liquids, series Encyclopedia of Physics, Springer, Berlin, Heidelberg. 1960; 3/10:134-280.
- Rowlinson JS, Widom B. Molecular Theory of Capillarity, Oxford University Press, Oxford. 1989.
- Jaycock MJ, Parfitt GD. Chemistry of Interfaces, Halstead Press, John Wiley & Sons, New York. 1981.
- Adamson AW, Gast AP. Physical Chemistry of Surfaces, Wiley-Interscience Publication, John Wiley & Sons. 1997.
- Rusanov AI, Prokhorov VA. Interfacial Tensiometry, Elsevier, Amsterdam. 1996.
- Baranov SA, Dikusar AI. Kinetics of Electrochemical Nanonucleation upon Induced Codeposition of Iron-Group Metals with Refractory Metals (W, Mo, Re).Surface Engineering and Applied Electrochemistry. 2022; 589(5):429-439. DOI: 10.3103/S1068375522050027.
- Baranov SA. Surface energy for nanowire. Annals of Mathematics and Physics. 2022; 81-86. DOI: 10.17352/amp.000043.
- Baranov SA. Surface Energy, and Production Micro-and Nanowire. Journal of Nanosciences Research & Reports 2022; 4(4):1-4. DOI: doi.org/10.47363/JNSRR/2022(4)142.
- Baranov SA, Rekhviashvili SSh, Sokurov AA. Some problems of simulation of the thermodynamic properties of droplets.Surface Engineering and Applied Electrochemistry. 2019;55(3):286-193. DOI: 10.5281/zenodo.1228887.
- Sears GW. A grown mechanism for mercury whiskers. Acta metallurgical. 1955; 3(4):367-369.
- Cahn RW. Background to rapid solidification processing. Liebermann HH. (ed.) Rapidly Solidified Alloys, Materials Engineering Series. Dekker, Parsippany, NJ. 1993; 3:1-15.
- Khachaturyan AG. Theory of structural transformations in solids, Dover Publications, New York. 2008.